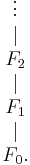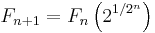Tower of fields
In mathematics, a tower of fields is a sequence of field extensions
- F0 ⊆ F1 ⊆ ... ⊆ Fn ⊆ ...
The name refers to the fact that such sequences are often written as
A tower of fields is called infinite if it is an infinite sequence, otherwise it is called finite.
Examples
- Q ⊆ R ⊆ C is a finite tower with rational, real and complex numbers.
- The sequence obtained by letting F0 be the rational numbers Q, and letting
- If p is a prime number the pth cyclotomic tower of Q is obtained by letting F0 = Q and Fn be the field obtained by adjoining to Q the pnth roots of unity. This tower is of fundamental importance in Iwasawa theory.
- The Golod–Shafarevich theorem shows that there are infinite towers obtained by iterating the Hilbert class field construction to a number field.
References
- Section 4.1.4 of Escofier, Jean-Pierre (2001), Galois theory, Graduate Texts in Mathematics, 204, Springer-Verlag, ISBN 978-0-387-98765-1